10.3. Функциональные связи. Построение уравнения регрессии. Линейная регрессия. Определение параметров уравнений регрессии методом наименьших квадратов.

 

     В естественных науках часто речь идет о функциональной зависимости (связи), когда каждому значению одной переменной соответствует вполне определенное значение другой. Функциональная зависимость может иметь место как между детерминированными (неслучайными) переменными (например, зависимость скорости падения в вакууме от времени), так и между случайными величинами (например, зависимость стоимости проданных изделий от их числа).

     В экономике в большинстве случаев между переменными величинами существует зависимость, когда каждому значению одной переменной соответствует не какое-то определенное, а множество возможных значений другой переменной. Иначе говоря, каждому значению одной переменной соответствует определенное распределение другой переменной. Такая зависимость получила название статистической.

Статистическая зависимость между двумя переменными, при которой каждому значению одной переменной соответствует определенное значение, т.е. математическое ожидание другой, называется корреляционной.

Корреляционная зависимость может быть представлена виде M_x(Y)=φ(x)  или M_y(X)=ψ(y).                                                                                                             (1)

      Предполагается, что   φ(x)≠const, ψ(y)≠const, т.е. если при изменении x или y условные математические ожидания M_x(Y) и M_y(X) не изменяются, то говорят, что корреляционная зависимость между переменными X иY отсутствует.

Уравнения (1) называются модлеьными уравнениями регрессии соответственно y по x и x по y, функции φ(x), ψ(y) – модельными функциями регрессии, а их графики – модельными линиями регрессии.

     Оценка функций регрессии φ(x), ψ(y) по выборке являются выборочные линии регрессии Y по X и X по Y: ; ,                    (2)

где – условная средняя переменной Y(X) при фиксированном значении переменной X=x(Y-y);  и – параметры кривой.

     Уравнения (2) называют выборочными уравнениями регрессии соответственно Y по X и X по Y. Параметры этих уравнений находятся с помощью метода наименьших квадратов.

     В случае линейной зависимости между двумя переменными уравнения регрессии Y по X и X по Y имеют вид:

; ,                                                                                    (3)

где  ;  – средние значения переменных                                       (4)

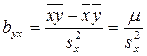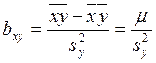;  – коэффициенты регрессии Y по X и X по Y   (5)

; – дисперсии переменных                                       (6)

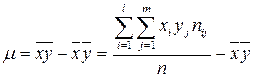 – выборочная ковариация переменных, где l и m – число различных значений x_i   и   y_j;  n_i и n_j – частоты значений  x_i   и   y_j; n_ij – частоты пар значений (x_i,y_j), причем .

Пример. Рассматривается зависимость между суточной выработкой продукции Y(т) и веоичиной основных производственных фондов X (млн руб.) для совокупности 50 однотипных предприятий.

Величина ОПФ (Х), млн руб.	Середины интервалов		Суточная выработка продукции (Y), т					Всего ni	Групповая средняя (
			7-11	11-15	15-19	19-23	13-27
	xi	yi	9	13	17	21	25
20-25	22,5		2	1	–	–	–	3	10,3
25-30	27,5		3	36	4	–	–	13	13,3
30-35	32,5		–	3	11	7	–	21	17,8
35-40	37,5		–	1	2	6	2	11	20,3
40-45	42,5		–	–	–	1	1	2	23
Всего nj			5	11	17	14	3	50	–
Групповая средняя , млн руб.			25,5	29,3	31,9	35,4	39,2	–	–

 

Необходимо найти уравнение регрессии Y по X и X по Y, коэффициенты корреляции между X и Y.

Решение:

;

;

;

;

.

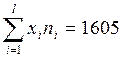Найдем выборочные характеристики и параметры уравнений регрессии:

;

;

;

;

;

;

.

Итак, уравнение регрессии:

, .

Вывод. Из первого уравнения регрессии следует, что при увеличении основных производственных фондов X на 1 млн руб. суточная выработка продукции Y предприятия увеличивается в среднем на 0,6762 т. Второе уравнение регрессии показывает, что для увеличения суточной выработки продукции Y на 1 т необходимо в среднем увеличить ОПФ X на 0,8099 млн руб. Коэффициент корреляции r=0,74, т.е. связь между X и Y прямая и достаточно тесная.

         Данные о статистической зависимости удобно задавать в виде корреляционной таблицы.

         Рассмотрим в качестве примера зависимость между суточной выработкой продукции Y (т) и величиной основных производственных фондов X (млн руб.) для совокупности 50 однотипных предприятий.

Величина ОПФ, млн. руб. (X)	Середины интервалов	Суточная выработка продукции, т (Y)					Всего ni	Групповая средняя, т
		7-11	11-15	15-19	19-23	23-27
	yi        xj	9	13	17	21	25
20-25 25-30 30-35 35-40 40-45	22,5 27,5 32,5 37,5 42,5	2 3 - - -	1 6 3 1 -	- 4 11 2 -	- - 7 6 1	- - - 2 1	3 13 21 11 2	10,3 13,3 17,8 20,3 23,0
Всего nj		5	11	17	14	3	50	-
Групповая средняя , млн руб.		25,5	29,3	31,9	35,4	39,2	-	-

 

             Изобразим полученную зависимость графически точками координатной плоскости. Сначала отметим средние  и соединим их ломаной, называемой эмпирической линией регрессии Y по X, а затем средние . Такое изображение статистической зависимости называется полем корреляции.

Неизвестные параметры уравнения линейной регрессии можно искать, применяя метод наименьших квадратов, согласно которому неизвестные параметры b₀ и b₁ выбираются таким образом, чтобы сумма квадратов отклонений эмпирических групповых средних , была минимальной:

.

    Коэффициент b₁ в уравнении регрессии, называется выборочным коэффициентом регрессии Y по X , который показывает, на сколько единиц в среднем изменится переменная Y при увеличении переменной X на одну единицу.

, .