ЛЕКЦИЯ 7

3. Поверхности (продолжение)

3.3. Общие рекомендации к решению задач на пересечение поверхностей

Задачи по построению линии пересечения поверхностей относятся к позиционным задачам. В общем случае решение этих задач сводится к определению множества точек, принадлежащих обеим поверхностям. Основной способ определения общих точек — способ вспомогательных секущих плоскостей.

Линия пересечения двух кривых поверхностей в общем случае представляет собой плавную пространственную кривую линию.

Линия пересечения кривой поверхности с многогранной в общем случае представляет собой совокупность плоских кривых, преломляющихся на ребрах многогранника.

Линия пресечения двух многогранных поверхностей в общем случае представляет собой пространственную ломаную линию, преломляющуюся на ребрах многогранников.

При решении задач на пересечение поверхностей необходимо учитывать, что в условии дано монолитное тело, ограниченное поверхностями и плоскостями. Никаких линий внутри тела не существует.

3.4. Линии и точки, принадлежащие поверхности

Точка принадлежит поверхности, если она принадлежит линии, лежащей на этой поверхности. В общем случае для определения недостающей проекции точки, принадлежащей поверхности, через данную точку проводят линию по поверхности, и находят искомую проекцию точки на одноименной проекции линии (рис.1). Точки, обозначение которых заключены в скобки, расположены на невидимой части поверхности. Вспомогательной линией может быть кривая линия или прямая, если поверхность линейчатая.

Примечание: К линейчатым относятся поверхности, в образовании которых участвует прямая линия. Примеры: коническая, цилиндрическая, торсовая поверхности, однополостный гиперболоид вращения, цилиндроид, коноид, гиперболический параболоид.

Рис. 1. Построение точек, принадлежащих поверхностям

3.5. Пересечение поверхности плоскостью

3.5.1. Конические сечения 

При пересечении поверхности прямого кругового конуса различными плоскостями образуются следующие линии (рис. 2):

1. Окружность, если секущая плоскость перпендикулярна оси конуса.

2. Эллипс, если секущая плоскость не параллельна ни одной из образующих конуса.

3. Две прямые линии (образующие), если секущая плоскость проходит через вершину конуса.

4. Парабола, если секущая плоскость параллельна только одной образующей конуса.

5. Гипербола, если секущая плоскость параллельна двум образующим конуса.

Рис. 2. Конические сечения

3.5.2. Цилиндрические сечения 

При пересечении поверхности прямого кругового цилиндра различными плоскостями образуются следующие линии (рис. 3):

1. Окружность, если секущая плоскость перпендикулярна оси цилиндра.

2. Эллипс, если секущая плоскость наклонена к оси цилиндра.
На рисунке 33 натуральная величина эллипса найдена способом совмещения.

3. Две прямые линии, если секущая плоскость параллельна оси цилиндра или проходит через нее.

Примечание: Если плоскость касается поверхности цилиндра, то общей для них является одна образующая.

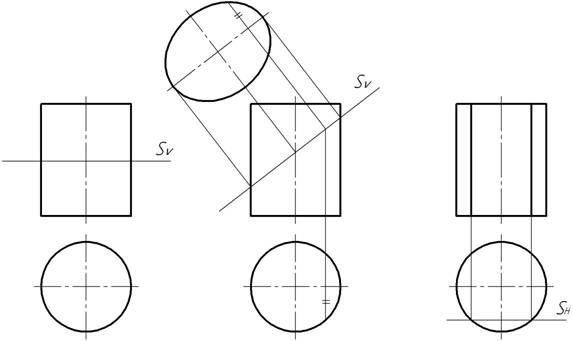
Рис. 3. Цилиндрические сечения

3.5.3. Сечение сферы

Плоскость пересекает сферу по окружности. Проекциями окружности могут быть окружность, эллипс, отрезок прямой линии. Если сферу рассекать плоскостью уровня, одна из проекций линии сечения будет окружностью, а другая — отрезком (рис. 4).

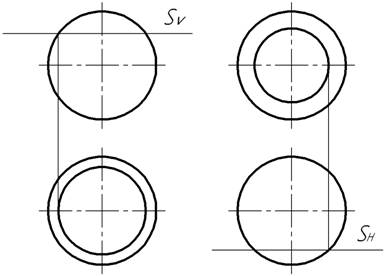
Рис. 4. Сечения сферы плоскостями уровня

Построим линию сечения сферы фронтально-проецирующей плоскостью. Окружность сечения на фронтальную плоскость проекций проецируется в виде отрезка, а на горизонтальную — в виде эллипса (рис. 5).

Рис. 5. Сечение сферы фронтально-проецирующей плоскостью   

3.6. Способ секущих плоскостей

Алгоритм определения общих точек двух пересекающихся поверхностей с помощью секущей плоскости:

1. Пересекаем обе заданные поверхности плоскостью.

2. Строим линии пересечения этой плоскости с каждой поверхностью
в отдельности.

3. Определяем точки пересечения построенных линий.

Обычно в качестве секущих применяют плоскости уровня. Их следует направлять таким образом, чтобы при пересечении с заданными поверхностями получались простые в построении линии — прямые, окружности.

Построение линии пересечения поверхностей рекомендуется начать с характерных точек ее проекций. Характерными точками проекции линии пересечения являются:

– точки, принадлежащие очерковым образующим поверхностей.

– экстремальные точки (высшая и низшая).

С помощью нескольких вспомогательных плоскостей находят ряд общих точек, соединив которые получают линию пересечения поверхностей.

Пример построения приведен на рисунке 6.

Рис. 6. Построение линий пересечения поверхностей геометрического тела

Видимость проекций линии пересечения определяют по отдельности. Взгляд наблюдателя в направлении проецирования выявляет видимые части поверхностей монолитного тела, и линии на них также будут видимыми.

3.5. Частные случаи пересечения поверхностей

Поверхность вращения – поверхность, полученная при вращении криволинейной или прямолинейной образующей вокруг неподвижной оси. Наиболее распространенными поверхностями  вращения являются: поверхность прямого кругового конуса, поверхность прямого кругового цилиндра, сфера, тор,  эллипсоид, параболоид вращения, гиперболоид вращения.

Если оси двух пересекающихся поверхностей вращения совпадают, то линии их пересечения являются окружностями, плоскости которых перпендикулярны оси (рис. 7).

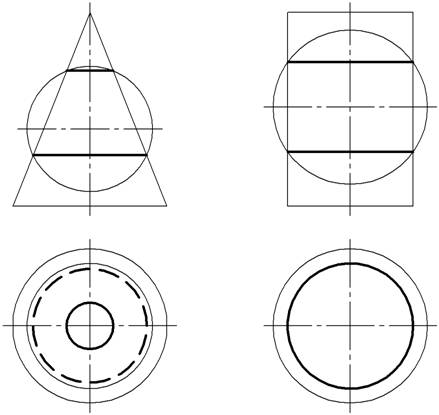
Рис. 7. Пересечение соосных поверхностей  вращения

Поверхность второго порядка — множество точек пространства, декартовые координаты которых удовлетворяют алгебраическому уравнению второй степени.

Примечание: Аналитически порядок поверхности определяется степенью ее уравнения. Геометрически — числом точек пересечения поверхности с прямой.

К таким поверхностям можно отнести перечисленные выше поверхности вращения (кроме тора), а также гиперболический параболоид, трехосный эллипсоид и др. Две поверхности второго порядка в общем случае пересекаются по пространственной кривой линии четвертого порядка.

Примечание: Степень алгебраического уравнения называется порядком кривой.. Геометрически порядок плоской кривой определяется числом точек пересечения ее с прямой линией. Порядок пространственной кривой определяется числом точек пересечения этой линии с плоскостью.

Кривая четвертого порядка может распадаться на две плоские кривые второго порядка.

Если оси поверхностей вращения второго порядка пересекаются и параллельны плоскости проекций, то линия их пересечения проецируется на эту плоскость в виде плоской кривой второго порядка.

Теорема Монжа. Если две поверхности второго порядка описаны вокруг третьей или вписаны в нее, то линия их пересечения распадается на две плоские кривые второго порядка. Плоскости этих кривых проходят через прямую, соединяющую точки пересечения линий касания (рис. 8).

Рис. 8. Пересечение поверхностей по теореме Монжа